Seam Carving

• Spec
• FAQ
• Project
• Submit

Although the underlying algorithm is simple and elegant, it was not discovered until 2007. Now, it is now a core feature in Adobe Photoshop and other computer graphics applications.

In this assignment, you will create a data type that resizes a W-by-H image using the seam-carving technique.

Finding and removing a seam involves three parts and a tiny bit of notation:

0. Notation. In image processing, pixel (x, y) refers to the pixel in column x and row y, with pixel (0, 0) at the upper left corner and pixel (W − 1, H − 1) at the bottom right corner. This is consistent with the Picture data type in algs4.jar. Warning: this is the opposite of the standard mathematical notation used in linear algebra where (i, j) refers to row i and column j and with Cartesian coordinates where (0, 0) is at the lower left corner.

   a 3-by-4 image

   (0, 0)	(1, 0)	(2, 0)
   (0, 1)	(1, 1)	(2, 1)
   (0, 2)	(1, 2)	(2, 2)
   (0, 3)	(1, 3)	(2, 3)

   We also assume that the color of a pixel is represented in RGB space, using three integers between 0 and 255. This is consistent with the java.awt.Color data type.

1. Energy calculation. The first step is to calculate the energy of each pixel, which is a measure of the importance of each pixel—the higher the energy, the less likely that the pixel will be included as part of a seam (as we'll see in the next step). In this assignment, you will implement the dual-gradient energy function, which is described below. Here is the dual-gradient energy function of the surfing image above:
   

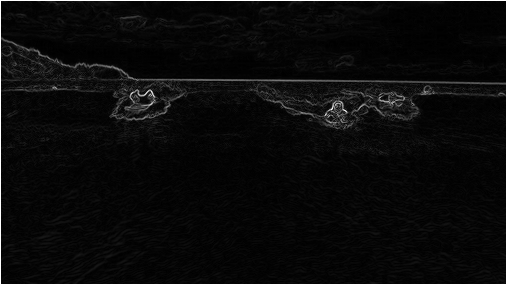
   The energy is high (white) for pixels in the image where there is a rapid color gradient (such as the boundary between the sea and sky and the boundary between the surfing Josh Hug on the left and the ocean behind him). The seam-carving technique avoids removing such high-energy pixels.

2. Seam identification. The next step is to find a vertical seam of minimum total energy. This is similar to the classic shortest path problem in an edge-weighted digraph except for the following:

   • The weights are on the vertices instead of the edges.

   • We want to find the shortest path from any of the W pixels in the top row to any of the W pixels in the bottom row.

   • The digraph is acyclic, where there is a downward edge from pixel (x, y) to pixels (x − 1, y + 1), (x, y + 1), and (x + 1, y + 1), assuming that the coordinates are in the prescribed range.
   
3. Seam removal. The final step is to remove from the image all of the pixels along the seam.

The SeamCarver API. Your task is to implement the following mutable data type:

public class SeamCarver {

   // create a seam carver object based on the given picture
   public SeamCarver(Picture picture)

   // current picture
   public Picture picture()

   // width of current picture
   public int width()

   // height of current picture
   public int height()

   // energy of pixel at column x and row y
   public double energy(int x, int y)

   // sequence of indices for horizontal seam
   public int[] findHorizontalSeam()

   // sequence of indices for vertical seam
   public int[] findVerticalSeam()

   // remove horizontal seam from current picture
   public void removeHorizontalSeam(int[] seam)

   // remove vertical seam from current picture
   public void removeVerticalSeam(int[] seam)

   //  unit testing (optional)
   public static void main(String[] args)

}

• Corner cases. Your code should throw an IllegalArgumentException when a constructor or method is called with an invalid argument, as documented below:

  • By convention, the indices x and y are integers between 0 and width − 1 and between 0 and height − 1 respectively, where width is the width of the current image and height is the height. Throw an IllegalArgumentException if either x or y is outside its prescribed range.

  • Throw an IllegalArgumentException if the constructor, removeVerticalSeam(), or removeHorizontalSeam() is called with a null argument.

  • Throw an IllegalArgumentException if removeVerticalSeam() or removeHorizontalSeam() is called with an array of the wrong length or if the array is not a valid seam (i.e., either an entry is outside its prescribed range or two adjacent entries differ by more than 1).

  • Throw an IllegalArgumentException if removeVerticalSeam() is called when the width of the picture is less than or equal to 1 or if removeHorizontalSeam() is called when the height of the picture is less than or equal to 1.

• Constructor. The data type may not mutate the Picture argument to the constructor.

• Computing the energy of a pixel. You will use the dual-gradient energy function: The energy of pixel \((x, y)\) is \(\sqrt{\Delta_x^2(x, y) + \Delta_y^2(x, y)}\), where the square of the x-gradient \(\Delta_x^2(x, y) = R_x(x, y)^2 + G_x(x, y)^2 + B_x(x, y)^2\), and where the central differences \(R_x(x, y)\), \(G_x(x, y)\), and \(B_x(x, y)\) are the differences in the red, green, and blue components between pixel (x + 1, y) and pixel (x − 1, y), respectively. The square of the y-gradient \(\Delta_y^2(x, y)\) is defined in an analogous manner. We define the energy of a pixel at the border of the image to be 1000, so that it is strictly larger than the energy of any interior pixel.

  As an example, consider the 3-by-4 image (supplied as 3x4.png) with RGB values—each component is an integer between 0 and 255—as shown in the table below:

  

  The ten border pixels have energy 1000. Only the pixels (1, 1) and (1, 2) are nontrivial. We calculate the energy of pixel (1, 2) in detail:

  R_x(1, 2) = 255 − 255 = 0,
  G_x(1, 2) = 205 − 203 = 2,
  B_x(1, 2) = 255 − 51 = 204,
  yielding Δ_x²(1, 2) = 2² + 204² = 41620.

  R_y(1, 2) = 255 − 255 = 0,
  G_y(1, 2) = 255 − 153 = 102,
  B_y(1, 2) = 153 − 153 = 0,
  yielding Δ_y²(1, 2) = 102² = 10404.

  Thus, the energy of pixel (1, 2) is \(\sqrt{41620 + 10404} = \sqrt{52024}\). Similarly, the energy of pixel (1, 1) is \(\sqrt{204^2 + 103^2}= \sqrt{52225}\).
  

• Finding a vertical seam. The findVerticalSeam() method returns an array of length H such that entry y is the column number of the pixel to be removed from row y of the image. For example, the dual-gradient energies of a 6-by-5 image (supplied as 6x5.png).
  

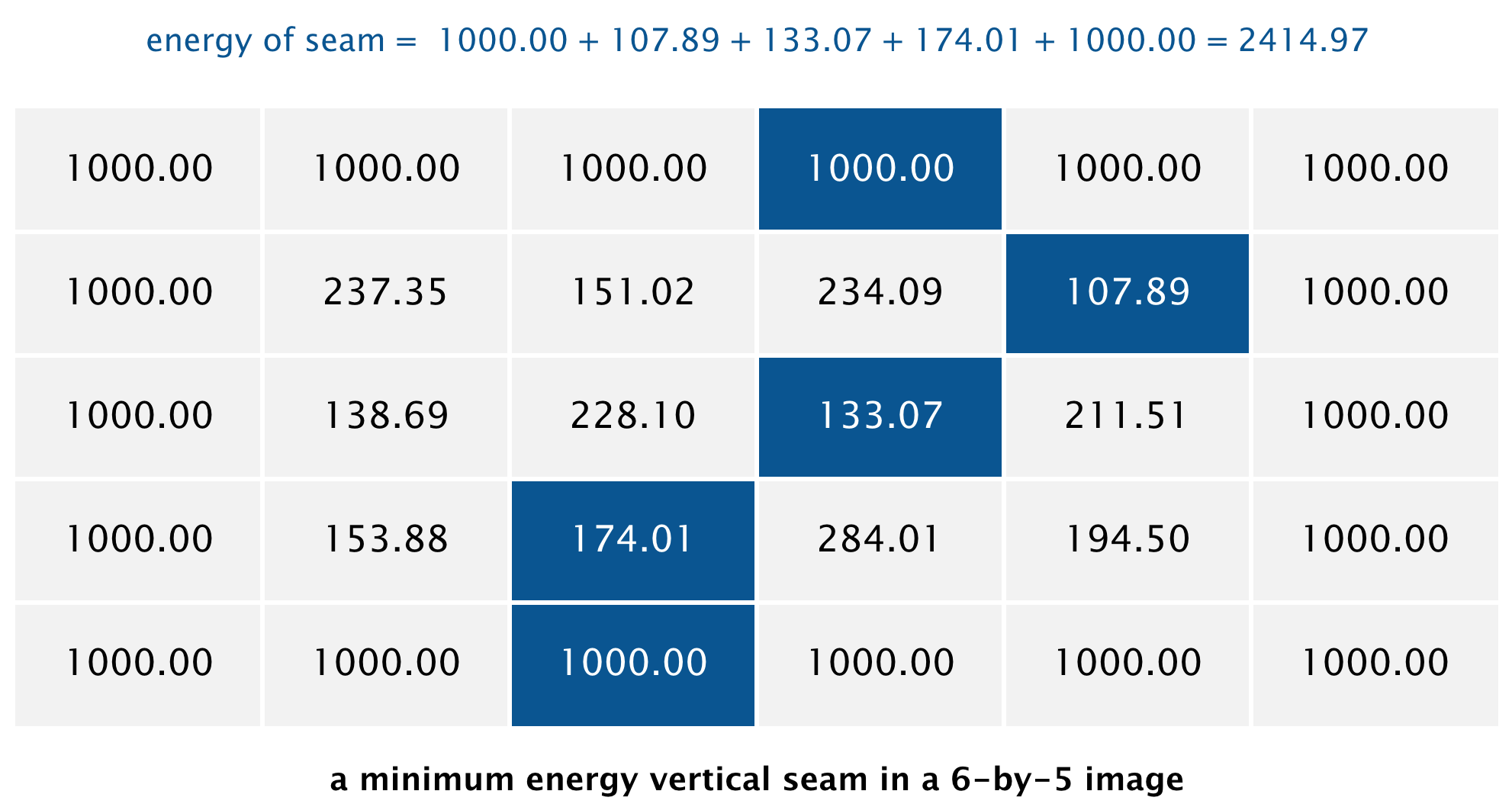
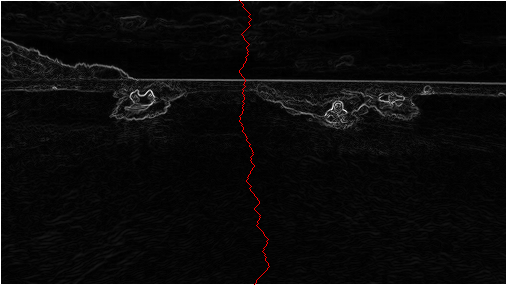
  The minimum energy vertical seam is highlighted in blue. In this case, the method findVerticalSeam() returns the array { 3, 4, 3, 2, 2 } because the pixels in a minimum energy vertical seam are (3, 0), (4, 1), (3, 2), (2, 3), and (2, 4). When there are multiple vertical seams with minimal total energy, your method can return any such seam.

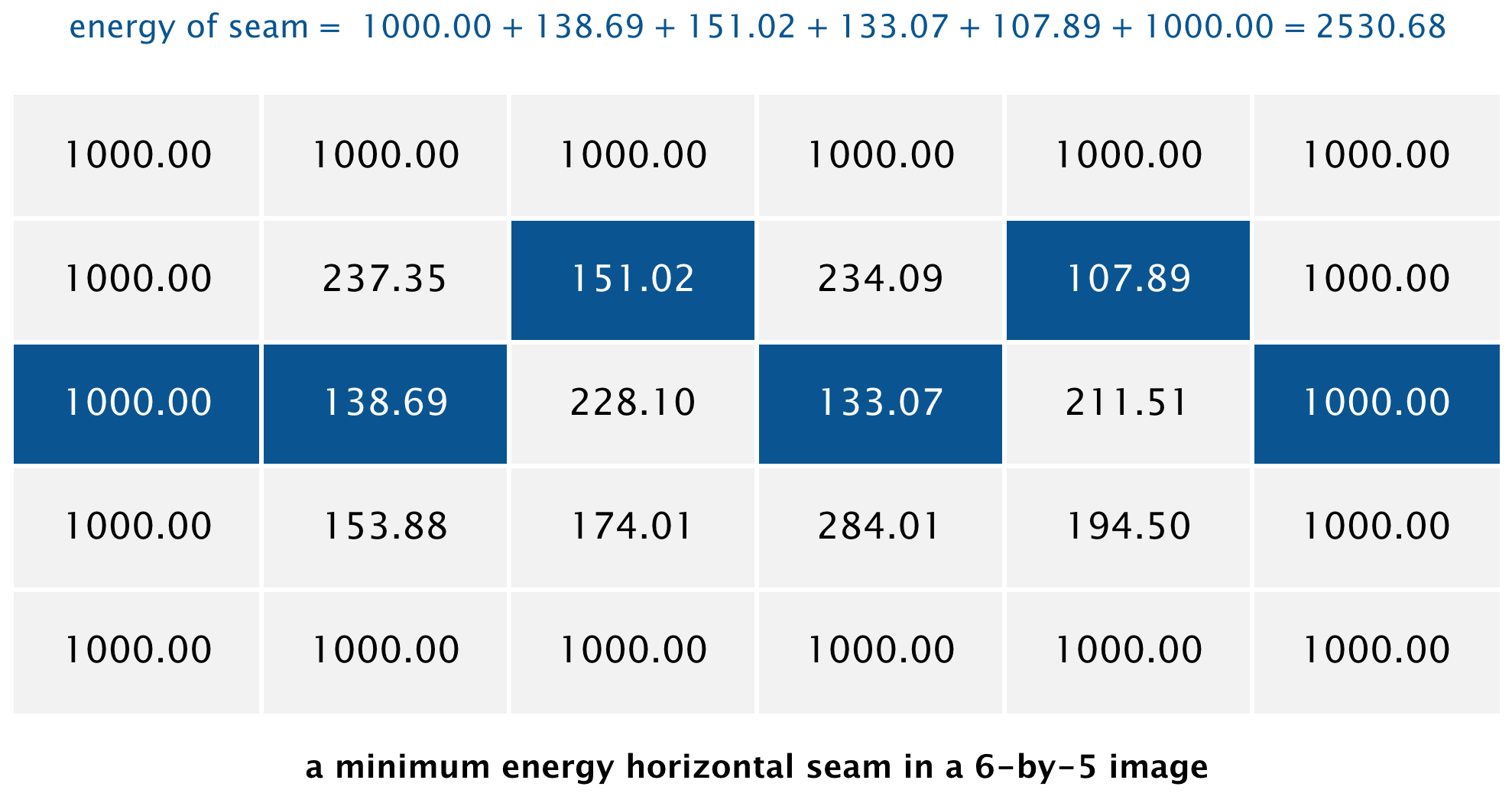
• Finding a horizontal seam. The behavior of findHorizontalSeam() is analogous to that of findVerticalSeam() except that it returns an array of length width such that entry x is the row number of the pixel to be removed from column x of the image. For the 6-by-5 image, the method findHorizontalSeam() returns the array { 2, 2, 1, 2, 1, 2 } because the pixels in a minimum energy horizontal seam are (0, 2), (1, 2), (2, 1), (3, 2), (4, 1), and (5, 2).

  

• Performance requirements. The width(), height(), and energy() methods should take constant time in the worst case. All other methods should run in time at most proportional to width × height in the worst case. For faster performance, do not construct explicit DirectedEdge and EdgeWeightedDigraph objects.

Analysis of running time (optional and not graded). 

• Give the worst-case running time to remove r rows and c columns from a width-by-height image as a function of r, c, width, and height.

• Estimate empirically the running time (in seconds) to remove r rows and c columns from a width-by-height image as a function of r, c, width, and H. Use tilde notation to simplify your answer.

Web submission. Submit a .zip file containing SeamCarver.java and any other supporting files (excluding algs4.jar and SCUtility.java). You may not call any library functions except those in java.lang, java.util, java.awt.Color, and algs4.jar.