Programming Assignment 3: Collinear Points

Write a program to recognize line patterns in a given set of points.

Computer vision involves analyzing patterns in visual images and reconstructing the real-world objects that produced them. The process is often broken up into two phases: feature detection and pattern recognition. Feature detection involves selecting important features of the image; pattern recognition involves discovering patterns in the features. We will investigate a particularly clean pattern recognition problem involving points and line segments. This kind of pattern recognition arises in many other applications such as statistical data analysis.

The problem. Given a set of n distinct points in the plane, find every (maximal) line segment that connects a subset of 4 or more of the points.

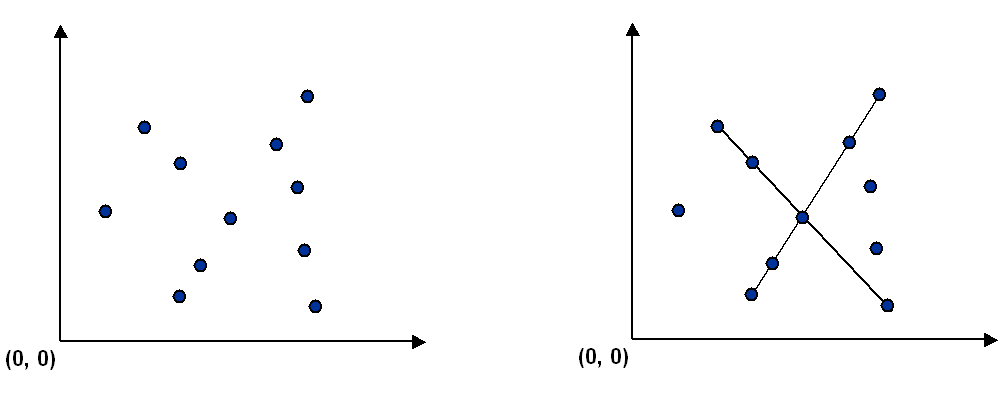
Point data type. Create an immutable data type Point that represents a point in the plane by implementing the following API:

public class Point implements Comparable<Point> {
   public Point(int x, int y)                         // constructs the point (x, y)

   public   void draw()                               // draws this point
   public   void drawTo(Point that)                   // draws the line segment from this point to that point
   public String toString()                           // string representation

   public               int compareTo(Point that)     // compare two points by y-coordinates, breaking ties by x-coordinates
   public            double slopeTo(Point that)       // the slope between this point and that point
   public Comparator<Point> slopeOrder()              // compare two points by slopes they make with this point
}

To get started, use the data type Point.java, which implements the constructor and the draw(), drawTo(), and toString() methods. Your job is to add the following components.

The compareTo() method should compare points by their y-coordinates, breaking ties by their x-coordinates. Formally, the invoking point (x₀, y₀) is less than the argument point (x₁, y₁) if and only if either y₀ < y₁ or if y₀ = y₁ and x₀ < x₁.
The slopeTo() method should return the slope between the invoking point (x₀, y₀) and the argument point (x₁, y₁), which is given by the formula (y₁ − y₀) / (x₁ − x₀). Treat the slope of a horizontal line segment as positive zero; treat the slope of a vertical line segment as positive infinity; treat the slope of a degenerate line segment (between a point and itself) as negative infinity.
The slopeOrder() method should return a comparator that compares its two argument points by the slopes they make with the invoking point (x₀, y₀). Formally, the point (x₁, y₁) is less than the point (x₂, y₂) if and only if the slope (y₁ − y₀) / (x₁ − x₀) is less than the slope (y₂ − y₀) / (x₂ − x₀). Treat horizontal, vertical, and degenerate line segments as in the slopeTo() method.
Do not override the equals() or hashCode() methods.

Corner cases. To avoid potential complications with integer overflow or floating-point precision, you may assume that the constructor arguments x and y are each between 0 and 32,767.

Line segment data type. To represent line segments in the plane, use the data type LineSegment.java, which has the following API:

public class LineSegment {
   public LineSegment(Point p, Point q)        // constructs the line segment between points p and q
   public   void draw()                        // draws this line segment
   public String toString()                    // string representation
}

Brute force. Write a program BruteCollinearPoints.java that examines 4 points at a time and checks whether they all lie on the same line segment, returning all such line segments. To check whether the 4 points p, q, r, and s are collinear, check whether the three slopes between p and q, between p and r, and between p and s are all equal.

public class BruteCollinearPoints {
   public BruteCollinearPoints(Point[] points)    // finds all line segments containing 4 points
   public           int numberOfSegments()        // the number of line segments
   public LineSegment[] segments()                // the line segments
}

The method segments() should include each line segment containing 4 points exactly once. If 4 points appear on a line segment in the order p→q→r→s, then you should include either the line segment p→s or s→p (but not both) and you should not include subsegments such as p→r or q→r. For simplicity, we will not supply any input to BruteCollinearPoints that has 5 or more collinear points.

Corner cases. Throw an IllegalArgumentException if the argument to the constructor is null, if any point in the array is null, or if the argument to the constructor contains a repeated point.

Performance requirement. The order of growth of the running time of your program should be n⁴ in the worst case and it should use space proportional to n plus the number of line segments returned.

A faster, sorting-based solution. Remarkably, it is possible to solve the problem much faster than the brute-force solution described above. Given a point p, the following method determines whether p participates in a set of 4 or more collinear points.

Think of p as the origin.
For each other point q, determine the slope it makes with p.
Sort the points according to the slopes they makes with p.
Check if any 3 (or more) adjacent points in the sorted order have equal slopes with respect to p. If so, these points, together with p, are collinear.

Applying this method for each of the n points in turn yields an efficient algorithm to the problem. The algorithm solves the problem because points that have equal slopes with respect to p are collinear, and sorting brings such points together. The algorithm is fast because the bottleneck operation is sorting.

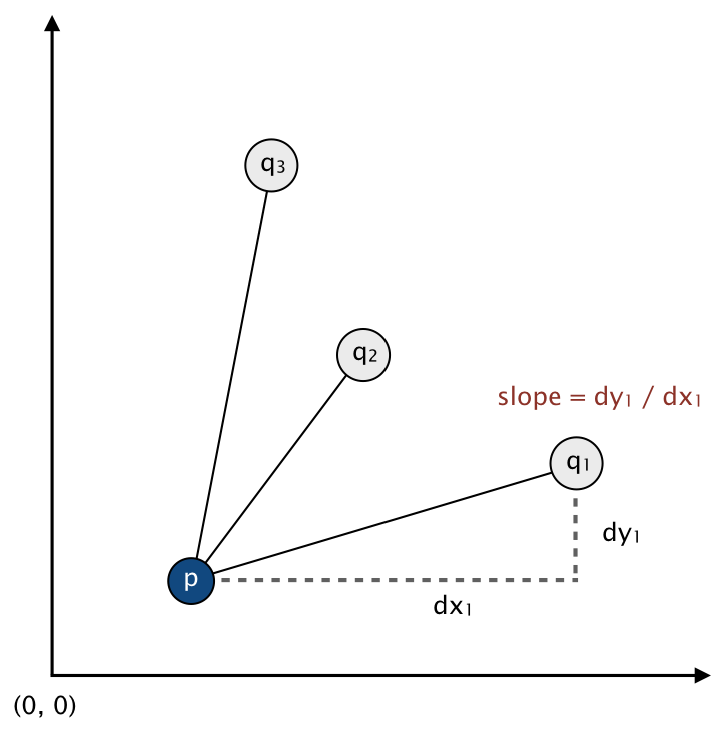
Write a program FastCollinearPoints.java that implements this algorithm.

public class FastCollinearPoints {
   public FastCollinearPoints(Point[] points)     // finds all line segments containing 4 or more points
   public           int numberOfSegments()        // the number of line segments
   public LineSegment[] segments()                // the line segments
}

The method segments() should include each maximal line segment containing 4 (or more) points exactly once. For example, if 5 points appear on a line segment in the order p→q→r→s→t, then do not include the subsegments p→s or q→t.

Corner cases. Throw an IllegalArgumentException if the argument to the constructor is null, if any point in the array is null, or if the argument to the constructor contains a repeated point.

Performance requirement. The order of growth of the running time of your program should be n² log n in the worst case and it should use space proportional to n plus the number of line segments returned. FastCollinearPoints should work properly even if the input has 5 or more collinear points.

Sample client. This client program takes the name of an input file as a command-line argument; read the input file (in the format specified below); prints to standard output the line segments that your program discovers, one per line; and draws to standard draw the line segments.

public static void main(String[] args) {

    // read the n points from a file
    In in = new In(args[0]);
    int n = in.readInt();
    Point[] points = new Point[n];
    for (int i = 0; i < n; i++) {
        int x = in.readInt();
        int y = in.readInt();
        points[i] = new Point(x, y);
    }

    // draw the points
    StdDraw.enableDoubleBuffering();
    StdDraw.setXscale(0, 32768);
    StdDraw.setYscale(0, 32768);
    for (Point p : points) {
        p.draw();
    }
    StdDraw.show();

    // print and draw the line segments
    FastCollinearPoints collinear = new FastCollinearPoints(points);
    for (LineSegment segment : collinear.segments()) {
        StdOut.println(segment);
        segment.draw();
    }
    StdDraw.show();
}

Input format. We supply several sample input files (suitable for use with the test client above) in the following format: An integer n, followed by n pairs of integers (x, y), each between 0 and 32,767. Below are two examples.

% cat input6.txt        % cat input8.txt
6                       8
19000  10000             10000      0
18000  10000                 0  10000
32000  10000              3000   7000
21000  10000              7000   3000
 1234   5678             20000  21000
14000  10000              3000   4000
                         14000  15000
                          6000   7000

% java-algs4 BruteCollinearPoints input8.txt
(10000, 0) -> (0, 10000) 
(3000, 4000) -> (20000, 21000) 

% java-algs4 FastCollinearPoints input8.txt
(3000, 4000) -> (20000, 21000) 
(0, 10000) -> (10000, 0)

% java-algs4 FastCollinearPoints input6.txt
(14000, 10000) -> (32000, 10000)

Web submission. Submit a .zip file containing only BruteCollinearPoints.java, FastCollinearPoints.java, and Point.java. We will supply LineSegment.java and algs4.jar. You may not call any library functions except those in java.lang, java.util, and algs4.jar. You may use library functions in java.util only if they have already been introduced in the course. For example, you may use Arrays.sort(), but not java.util.HashSet.